铝合金高频窄脉冲电化学抛光的研究
铝合金高频窄脉冲电化学抛光的研究
石鸽娅 丁必荣 沈健
(合肥工业大学机械与汽车工程学院,安徽合肥230009)
(合肥工业大学机械与汽车工程学院,安徽合肥230009)
摘要:为了研究铝合金高频窄脉冲电流电化学抛光中各抛光工艺参数与表面粗糙度之间的关系,采用正交试验法安排脉宽、抛光电压和抛光间隙等抛光工艺参数,用极差分析法初步定性地分析了各参数对表面质量影响的大小,然后运用逐步回归分析的方法建立数学模型,最终确定四次函数的回归方程(最优回归方程)为数学模型,并通过单因素试验验证了数学模型的可靠性,从而可对各工艺参数与表面粗糙度的关系作定量分析,为铝合金脉冲电流电化学抛光的研究和推广应用打下了一定的理论基础。
引 言
铝和铝合金性能优良,应用广泛,为提高其制品抗蚀性和表面装饰效果,必须进行抛光处理。常用抛光方法中,电化学抛光方法综合效果最佳。
脉冲电流电化学抛光是近年兴起的一门新技术,它是采用周期性间歇供电代替传统的连续直流供电,利用中性电解液为电解抛光液,使工具阴极与工件阳极之间保持较小加工间隙的一种工件表面抛光方法。与传统的直流电化学抛光相比,脉冲电流电化学抛光能引起一系列的脉冲效应,导致电化学抛光间隙过程理化特性的变化,从而提高了抛光精度,表面质量和抛光效率。试验研究表明。随着脉冲电流频率提高、脉宽变窄、占空比(数值)变小,脉冲效应加强,当频率达到千赫兹后,抛光效果有明显的提高。本文采用微秒级的高频窄脉冲电流对铝合金进行电化学抛光,来研究铝合金高频窄脉冲电流电化学抛光的工艺规律,并建立其数学模型。
1 铝合金高频窄脉冲电化学抛光的正交试验和极差分析
针对铝合金LF21,通过对比试验,选择8% NaNO3+6%Na2SO4的复合水溶液+少量乙醇、甘油等添加剂作为其脉冲电化学抛光的中性盐电解液。在电解液参数一定的情况下,脉冲电化学抛光的抛光质量主要与脉冲电流的宽度、脉冲占空比、抛光电压、抛光时间和抛光间隙有关。为了综合分析各影响因素与抛光后工件表面粗糙度Ra之间的关系,安排了一组正交试验,选取5个因素:脉宽tp、脉冲占空比tp/ts、抛光间隙δ、抛光时间t和抛光电压U。所有因素皆取5水平,选用/25r 55 J正交表,各参数的取值和正交试验的试验结果见表1,正交试验的极差分析见表2。
本试验的指标为表面粗糙度,数值越小越好。根据表2中极差D的大小可以看出,5个工艺参数对表面粗糙度Ra的影响
表1 脉冲电流电化学抛光实验结果
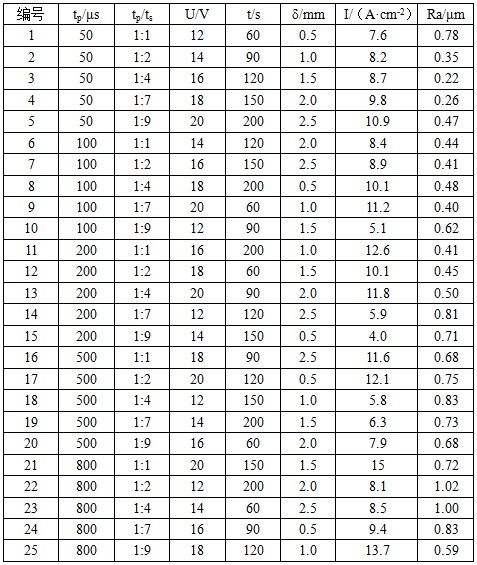
表2 脉冲电流电化学抛光实验结果极差分析表
由大到小依次为:脉宽、抛光电压、抛光间隙、抛光时间、脉冲占空比。对试验结果进行比较选优,可以得出表面粗糙度最小时各因素的取值分别为:脉宽50μs、脉冲占空比1:2、电压18V、时间120s、间隙1mm。采用以上优选数据重复进行了3次抛光试验,测得加工后的工件表面粗糙度稳定在0.20μm左右。
2 脉冲电流电化学抛光的逐步回归分析
根据正交试验的数据,采用逐步回归分析的方法,建立铝合金LF21脉冲电化学抛光的数学模型。在本系统中,回归方程的自变量有5个:脉宽tp、脉冲占空比tp/ts、抛光电压U、抛光时间t、间隙δ。因变量为抛光工件的表面粗糙度Ra。
本文选择了6种函数形态(一次函数、二次函数、含交叉项的二次函数、三次函数、四次函数、幂函数)进行逐步回归分析,求得回归方程后进行比较,选择其中可信度和准确度高并且简单的回归方程作为所求的数学模型。取置信度a=0.25,对表1中的试验数据进行回归分析,得到如下6个回归方程:
一次函数:(Ra/μm)=0.940+0.000544(tp/μs)-0.0321(U/V) (1)
二次函数:(Ra/μm)=3.554+0.001036(tp/μs-0.3761(U/V)-0.000000584(tp2/μs2)+0.01075( U2/V2) (2)
含交叉项的二次函数:(Ra/μm)=4.578+0.001481(tp/μs)-0.4911(U/V)-0.00289(t/s)-0.000000584(tp2/μs2)+0.01420(U2/V2)+0.0000148(t2/s2)-0.00000359(tp/μs)×(t/s) (3)
三次函数:(Ra/μm)=2.691+0.001036(tp/μs)-0.2078(U/V)-0.000000584(tp2/μs2)+0.00023( U3/V3) (4)
四次函数:(Ra/μm)=3.302+0.001036(tp/μs)-0.1519(U/V)-3.095( δ/mm) -0.000000584(tp2/μs2)+3.036(δ2/mm2)-1.261(δ3/mm3)+0.0000069(U4/V4)+0.192(δ4/mm4) (5)
幂函数:(Ra/μm )=e0.243(tp/μs)0.282(U/V)-0.842 (6)
回归方程中各变量系数小数点后的有效位数是根据该变量的数量级选取的。占空比tp/ts和抛光时间t对表面粗糙度Ra的作用不显著,因而在回归方程中不出现。
通过对6个回归方程的剩余平方和、相关系数、F检验值、标准偏差,残差进行分析和比较,确定最优回归方程为四次函数的回归方程(置信度a=0.25):(Ra/μm)=3.302+0.001036(tp/μs)-0.1519(U/V)-3.095(δ/mm)-0.000000584(tp2/μs2)+3.036(δ2/mm2)-1.261(δ3/mm3)+0.0000069(U4/V4)+0.192(δ4/mm4)
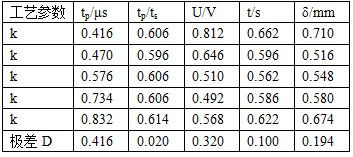
根据最优回归方程,可以对各自变量参数与表面粗糙度Ra值的关系作定量分析,变动1个自变量参数,可得到单个自变量参数变化时的关系曲线,如图1~图3所示。
脉冲电流电化学抛光是近年兴起的一门新技术,它是采用周期性间歇供电代替传统的连续直流供电,利用中性电解液为电解抛光液,使工具阴极与工件阳极之间保持较小加工间隙的一种工件表面抛光方法。与传统的直流电化学抛光相比,脉冲电流电化学抛光能引起一系列的脉冲效应,导致电化学抛光间隙过程理化特性的变化,从而提高了抛光精度,表面质量和抛光效率。试验研究表明。随着脉冲电流频率提高、脉宽变窄、占空比(数值)变小,脉冲效应加强,当频率达到千赫兹后,抛光效果有明显的提高。本文采用微秒级的高频窄脉冲电流对铝合金进行电化学抛光,来研究铝合金高频窄脉冲电流电化学抛光的工艺规律,并建立其数学模型。
1 铝合金高频窄脉冲电化学抛光的正交试验和极差分析
针对铝合金LF21,通过对比试验,选择8% NaNO3+6%Na2SO4的复合水溶液+少量乙醇、甘油等添加剂作为其脉冲电化学抛光的中性盐电解液。在电解液参数一定的情况下,脉冲电化学抛光的抛光质量主要与脉冲电流的宽度、脉冲占空比、抛光电压、抛光时间和抛光间隙有关。为了综合分析各影响因素与抛光后工件表面粗糙度Ra之间的关系,安排了一组正交试验,选取5个因素:脉宽tp、脉冲占空比tp/ts、抛光间隙δ、抛光时间t和抛光电压U。所有因素皆取5水平,选用/25r 55 J正交表,各参数的取值和正交试验的试验结果见表1,正交试验的极差分析见表2。
本试验的指标为表面粗糙度,数值越小越好。根据表2中极差D的大小可以看出,5个工艺参数对表面粗糙度Ra的影响
表1 脉冲电流电化学抛光实验结果

表2 脉冲电流电化学抛光实验结果极差分析表

由大到小依次为:脉宽、抛光电压、抛光间隙、抛光时间、脉冲占空比。对试验结果进行比较选优,可以得出表面粗糙度最小时各因素的取值分别为:脉宽50μs、脉冲占空比1:2、电压18V、时间120s、间隙1mm。采用以上优选数据重复进行了3次抛光试验,测得加工后的工件表面粗糙度稳定在0.20μm左右。
2 脉冲电流电化学抛光的逐步回归分析
根据正交试验的数据,采用逐步回归分析的方法,建立铝合金LF21脉冲电化学抛光的数学模型。在本系统中,回归方程的自变量有5个:脉宽tp、脉冲占空比tp/ts、抛光电压U、抛光时间t、间隙δ。因变量为抛光工件的表面粗糙度Ra。
本文选择了6种函数形态(一次函数、二次函数、含交叉项的二次函数、三次函数、四次函数、幂函数)进行逐步回归分析,求得回归方程后进行比较,选择其中可信度和准确度高并且简单的回归方程作为所求的数学模型。取置信度a=0.25,对表1中的试验数据进行回归分析,得到如下6个回归方程:
一次函数:(Ra/μm)=0.940+0.000544(tp/μs)-0.0321(U/V) (1)
二次函数:(Ra/μm)=3.554+0.001036(tp/μs-0.3761(U/V)-0.000000584(tp2/μs2)+0.01075( U2/V2) (2)
含交叉项的二次函数:(Ra/μm)=4.578+0.001481(tp/μs)-0.4911(U/V)-0.00289(t/s)-0.000000584(tp2/μs2)+0.01420(U2/V2)+0.0000148(t2/s2)-0.00000359(tp/μs)×(t/s) (3)
三次函数:(Ra/μm)=2.691+0.001036(tp/μs)-0.2078(U/V)-0.000000584(tp2/μs2)+0.00023( U3/V3) (4)
四次函数:(Ra/μm)=3.302+0.001036(tp/μs)-0.1519(U/V)-3.095( δ/mm) -0.000000584(tp2/μs2)+3.036(δ2/mm2)-1.261(δ3/mm3)+0.0000069(U4/V4)+0.192(δ4/mm4) (5)
幂函数:(Ra/μm )=e0.243(tp/μs)0.282(U/V)-0.842 (6)
回归方程中各变量系数小数点后的有效位数是根据该变量的数量级选取的。占空比tp/ts和抛光时间t对表面粗糙度Ra的作用不显著,因而在回归方程中不出现。
通过对6个回归方程的剩余平方和、相关系数、F检验值、标准偏差,残差进行分析和比较,确定最优回归方程为四次函数的回归方程(置信度a=0.25):(Ra/μm)=3.302+0.001036(tp/μs)-0.1519(U/V)-3.095(δ/mm)-0.000000584(tp2/μs2)+3.036(δ2/mm2)-1.261(δ3/mm3)+0.0000069(U4/V4)+0.192(δ4/mm4)
根据最优回归方程,可以对各自变量参数与表面粗糙度Ra值的关系作定量分析,变动1个自变量参数,可得到单个自变量参数变化时的关系曲线,如图1~图3所示。


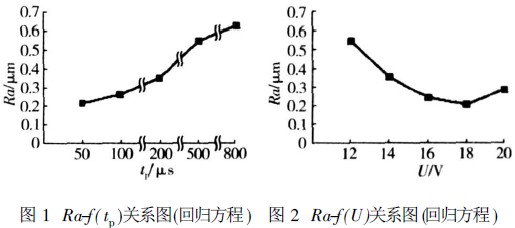
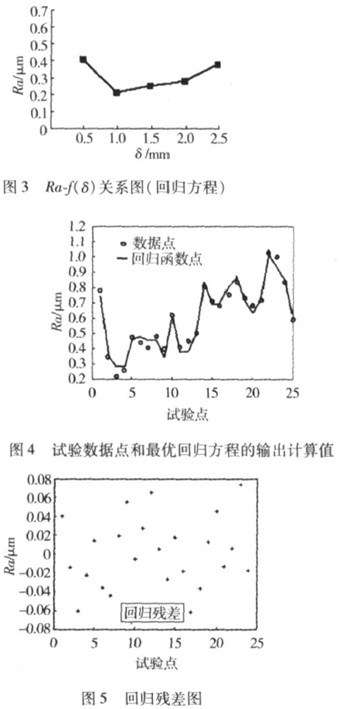
图4为试验数据点和最优回归方程的输出计算值。图5为试验数据点与最优回归方程输出计算值的残差图。从图4和图5可以看到,输出计算值和试验数据点基本吻合。
3 工艺参数对表面粗糙度的影响
3.1 脉冲宽度
如图1所示,随着脉冲宽度的减小,抛光质量有明显提高的趋势。在微秒级脉冲电流电化学抛光中,由于脉冲电流的间隙作用、阶跃变化,使加工间隙内的电解液发生振荡,产生压力波,压力波的搅拌作用大大地改善了加工间隙中电解液的流动条件,加速了间隙内电解液的更新,消除了加工间隙内电解液电导率分布的不均匀,从而提高了加工精度,减小了表面粗糙度。同时由于间隙内电解液的周期性更新,使间隙内的电化学产物能及时充分地排除,降低了电解液系统对加工质量的不利影响。
3.2 抛光电压
分析图2可知,在一定的条件下,存在着使表面粗糙度达到最小值的最佳抛光电压范围。电压过小,在较短时间内不能去除原表面上的微观不平度,生产率低,达不到迅速整平的目的;电压过大,阳极溶解太剧烈,超过了钝化区部分,而转向超钝化区,这不是抛光中希望出现的。故电压取18V左右效果最好。
3.3 抛光间隙
从图3可以看到,在其它因素固定时,抛光间隙也有一个最适宜的值。在实际抛光中,如果抛光间隙过大,当电流密度一定时,则极间电压需要随之增大,大量的电能要消耗于电解液的欧姆电阻,降低了电能的利用率,会使电解液温度升高,影响抛光质量;但抛光间隙也不能过小,否则易引起电化学抛光产物的阻塞,特别是产生的气体和热量排除不畅通,从而降低抛光质量。在我们的试验中,适宜的抛光间隙为1mm。
3.4 脉冲占空比
在微秒级脉冲宽度的情况下,脉冲电流的占空比对表面粗糙度的影响不明显,取1:2时可以兼顾抛光表面质量和抛光生产率。
3.5 抛光时间
抛光时间对表面质量也有一定的影响。随着抛光时间的延长,工件表面粗糙度开始是逐步减小的,但超过一定时间后又逐步增大,所以要恰当地选取抛光时间才能得到较好的抛光效果,选择120s时即能达到较好的加工质量。
4 单因素试验的验证
为了验证最优回归方程中的单个自变量参数变化时的关系曲线是否与实际情况一致,进行了一组单因素试验。在其它自变量参数最优的情况下,分别研究脉宽、抛光电压、抛光间隙这3个对抛光质量影响较大的因素与表面粗糙度之间的影响。结果如图6~图8所示。
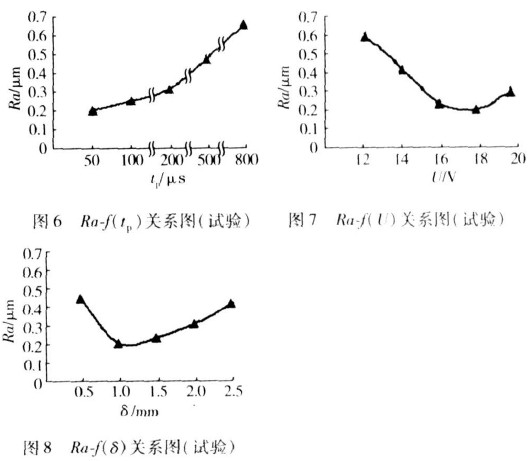
由图6可以看到,当其它因素固定时,增加脉宽,表面粗糙度数值由小变大,这也验证了前人试验所得出的结论:高频窄脉冲电流对改善抛光区中的流场是有利的。由图7可知,随着电压的升高,表面粗糙度先减小后增大,在18V时,表面粗糙度达到最小值。在单因 素变化曲线图8中,表面粗糙度是随着间隙的增大而先减小后增大的,故在进行电化学抛光时适宜的间隙为1mm。
3 工艺参数对表面粗糙度的影响
3.1 脉冲宽度
如图1所示,随着脉冲宽度的减小,抛光质量有明显提高的趋势。在微秒级脉冲电流电化学抛光中,由于脉冲电流的间隙作用、阶跃变化,使加工间隙内的电解液发生振荡,产生压力波,压力波的搅拌作用大大地改善了加工间隙中电解液的流动条件,加速了间隙内电解液的更新,消除了加工间隙内电解液电导率分布的不均匀,从而提高了加工精度,减小了表面粗糙度。同时由于间隙内电解液的周期性更新,使间隙内的电化学产物能及时充分地排除,降低了电解液系统对加工质量的不利影响。
3.2 抛光电压
分析图2可知,在一定的条件下,存在着使表面粗糙度达到最小值的最佳抛光电压范围。电压过小,在较短时间内不能去除原表面上的微观不平度,生产率低,达不到迅速整平的目的;电压过大,阳极溶解太剧烈,超过了钝化区部分,而转向超钝化区,这不是抛光中希望出现的。故电压取18V左右效果最好。
3.3 抛光间隙
从图3可以看到,在其它因素固定时,抛光间隙也有一个最适宜的值。在实际抛光中,如果抛光间隙过大,当电流密度一定时,则极间电压需要随之增大,大量的电能要消耗于电解液的欧姆电阻,降低了电能的利用率,会使电解液温度升高,影响抛光质量;但抛光间隙也不能过小,否则易引起电化学抛光产物的阻塞,特别是产生的气体和热量排除不畅通,从而降低抛光质量。在我们的试验中,适宜的抛光间隙为1mm。
3.4 脉冲占空比
在微秒级脉冲宽度的情况下,脉冲电流的占空比对表面粗糙度的影响不明显,取1:2时可以兼顾抛光表面质量和抛光生产率。
3.5 抛光时间
抛光时间对表面质量也有一定的影响。随着抛光时间的延长,工件表面粗糙度开始是逐步减小的,但超过一定时间后又逐步增大,所以要恰当地选取抛光时间才能得到较好的抛光效果,选择120s时即能达到较好的加工质量。
4 单因素试验的验证
为了验证最优回归方程中的单个自变量参数变化时的关系曲线是否与实际情况一致,进行了一组单因素试验。在其它自变量参数最优的情况下,分别研究脉宽、抛光电压、抛光间隙这3个对抛光质量影响较大的因素与表面粗糙度之间的影响。结果如图6~图8所示。

由图6可以看到,当其它因素固定时,增加脉宽,表面粗糙度数值由小变大,这也验证了前人试验所得出的结论:高频窄脉冲电流对改善抛光区中的流场是有利的。由图7可知,随着电压的升高,表面粗糙度先减小后增大,在18V时,表面粗糙度达到最小值。在单因 素变化曲线图8中,表面粗糙度是随着间隙的增大而先减小后增大的,故在进行电化学抛光时适宜的间隙为1mm。
由图6-图8可以看到,由回归方程得到的表面粗糙度Ra与t、U和δ的关系曲线图与由单因素试验得到的结论相吻合,而且与前面极差分析得到的结果是一致的,这说明了用逐步回归分析进行建模是成功的。
5 结论
(1)采用正交试验的方法可以用较少的试验次数得到比较全面的试验数据,采用极差分析可以对抛光的工艺规律作定性的分析:各因素对表面粗糙度Ra的影响由主到次顺序为tp→U→δ→t→tp/ts;较优的抛光参数为:脉宽50μs、脉冲占空比1:2、电压18V、时间120s、间隙1mm。
(2)根据正交试验的试验数据,采用逐步回归分析的方法,可以得到表面粗糙度Ra的最优回归方程(置信度a=0.25)。根据最优回归方程,可以对各自变量参数与Ra值的关系作定量分析。
(3)通过单因素试验验证了最优回归方程,建立了微秒级高频窄脉冲电流电化学抛光的数学模型,为今后铝合金电化学抛光技术的研究和推广应用提供了参考借鉴。
上一篇: 铝合金电化学抛光工艺现状
下一篇: 铝合金环保型无烟化学抛光工艺的研究

